Entropy and Kullback-Leibler Divergence:¶
Entropy:¶
In statistics, thermodynamics and information theory, entropy is a measure of uncertainty or information (the connection between uncertainty and information is that "an occurrence of an unlikely event gives you more information than the occurrence of a likely event"). The entropy of a discrete probability distribution with $n$ different outcomes, $p=\langle p_1, ..., p_n \rangle$, is:
$$H(p)=-\sum_{i=1}^{n} p_i \cdot \log_{2}p_i. \tag{1}$$For a continuous probability distribution, $p()$, the entropy is given by:
$$H(P)=-\int_\theta p(\theta) \cdot \log p(\theta) d\theta.$$For a multivariable Normal distribution:
$$H(p)=\sum_i \log \sigma_i.$$Cross-Entropy:¶
Cross-entropy is a measure of the relative entropy between two probability distributions over the same set of events.
$$ H(p, q)=-\sum_{i=1}^{n} p_i \cdot \log_{2}q_i. \tag{2} $$The cross-entropy is simply equal to the entropy, if the distributions $p$ and $q$ are equal. If the distributions $p$ and $q$ differ, then the cross-entropy will be larger than the entropy by some amount. The amount by which the cross-entropy value exceeds the entropy value is called the relative entropy, or KL-divergence.
KL-Divergence:¶
For two probability distributions: $p=\langle p_1, ..., p_n \rangle$ and $q=\langle q_1, ..., q_n \rangle$, the Kullback-Leibler Divergence between $p$ and $q$ is:
$$ \begin{align} D_{KL}(p \parallel q) &= \underbrace{H(p, q)}_{\text{Cross-entropy}} - \underbrace{H(p)}_{\text{Entropy}}, \\ &= \sum_{i=1}^{n} p_i (\log_2 p_i - \log_2 q_i).\tag{3} \end{align} $$This gives a measure of similarity or 'distance' between two probability distributions. Note that KL-divergence is not symmetric: $D_{KL}(p \parallel q) \neq D_{KL}(q \parallel p)$.
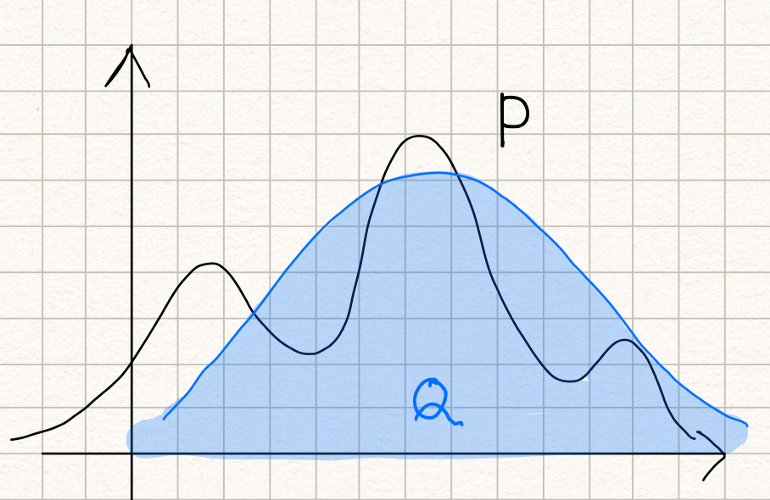
The KL-divergence value, $D_{KL}(P \parallel Q)$ is the measure of the 'mismatch' when we use probability distribution $Q$ to approximate the true probability distribution $P$
For continuous distributions, $p$ and $q$, KL-divergence is given by:
$$D_{KL}(p \parallel q) = \int_\theta p(\theta)(\log p(\theta) - \log q(\theta)) d\theta.$$Example Calculations:¶
Suppose we have a true probability distribution of different weather conditions and a predicted probability distribution:
|
True probability distribution $p$ 
|
Predicted probability distribution $q$ 
|
The entropy is of the true probability distribution is: $$ \begin{align} H(p) = &-\sum_{i=1}^{n} p_i \log_{2}p_i, \\ = &-\big( 0.35 \log_2 (0.35) + 0.35 \log_2 (0.35)\\ &+ 0.1 \log_2 (0.1) + 0.1 \log_2 (0.1)\\ &+ 0.04 \log_2 (0.04) + 0.04 \log_2 (0.04)\\ &+ 0.01 \log_2 (0.01) + 0.01 \log_2 (0.01)\big) = 2.22897\ldots. \end{align} $$
The cross-entropy is given by: $$ \begin{align} H(p, q) = &-\sum_i p_i \log_2 q_i \\ = &-\big( 0.35\log_2 0.01 + 0.35\log_2 (0.01)\\ &+ 0.1\log_2 0.04 + 0.1\log_2 0.04 \\ &+ 0.04\log_2 0.1 + 0.04\log_2 0.1 \\ &+ 0.01\log_2 0.35 + 0.01\log_2 0.35 \big) = 5.87551\ldots. \end{align} $$
The KL-divergence is given by: $$ \begin{align} D_{KL}(p \parallel q) &= \underbrace{H(p, q)}_{\text{Cross-entropy}} - \underbrace{H(p)}_{\text{Entropy}} \\ &= 5.87551\ldots - 2.22897\ldots \\ &= 3.64654\ldots. \end{align} $$
Another Example Calculation:¶
In the context of deep learning, suppose we an image classifer with 5 output classes and we are using cross-entropy loss as the error function.
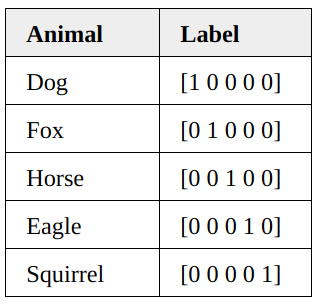
|

Suppose the true label vector is $p=[1, 0, 0, 0, 0]$ and the network's output vector is $q=[0.4, 0.3, 0.05, 0.05, 0.2]$. The cross-entropy loss value is calculated as: $$ \begin{align} H(p, q) &= -\big( 1\cdot\ln (0.4) + 0 + 0 + 0 + 0 \big) \\ &= 0.91629\ldots. \end{align} $$ Suppose now after training, the network's predictions are more accurate and produces the output vector $q=[0.98, 0.01, 0, 0, 0.01]$. Here the cross-entropy is: $$ \begin{align} H(p, q) &= -\big( 1\cdot\ln (0.98) + 0 + 0 + 0 + 0 \big) \\ &= 0.020207\ldots. \end{align} $$ |
Entropy and Huffman Encoding:¶
The concept of entropy was first introduced by Claude Shannon in 1948 in his paper title "A Mathematical Theory of Communication". The aim was to investigate the smallest possible average size of lossless encoding for messages transmitted from a source to a destination.
The entropy value of a frequency distribution of characters to send in a message, $H(p)$, gives the average number of bits required to represent a character drawn randomly from the message, in the most efficient character encoding scheme generated by Huffman's encoding algorithm.
Example 1. Suppose a message consists only of $A$ and $B$, both with equal frequency. The huffman encoding would assign $A=\texttt{0}$ and $B=\texttt{1}$, for example.
- The entropy value here would be $H(\langle 0.5, 0.5 \rangle)=-(0.5 \cdot \log_2\frac{1}{2} + 0.5 \cdot \log_2\frac{1}{2}) = 1 \texttt{ bit}$ .
Example 2. Suppose a message consists of $A, B \text{ and } C$ with frequencies $0.5, 0.25 \text{ and } 0.25$ respectively. The huffman encoding would assign $A=0, B=10, C=11$, for example.
- The entropy value here would be $H(\langle 0.5, 0.25, 0.25 \rangle)=-(0.5 \cdot \log_2\frac{1}{2} + 0.25 \cdot \log_2\frac{1}{4} + 0.25 \cdot \log_2\frac{1}{4}) = 1.5 \texttt{ bits}$.
Note: $D_{KL}(q \parallel p)$ is the number of 'extraneous' bits that would be transmitted if we designed an encoding scheme based on $q's$ frequency distribution but it turned out the samples would be drawn from $p's$ frequency distribution instead.
- Eg. If we designed a huffman encoding for the alphabet around the frequency distribution in English, but applied for German text, then the number of 'wastage' bits would be $D_{KL}(q \parallel p)$.
Forward/Reverse KL-Divergence:¶
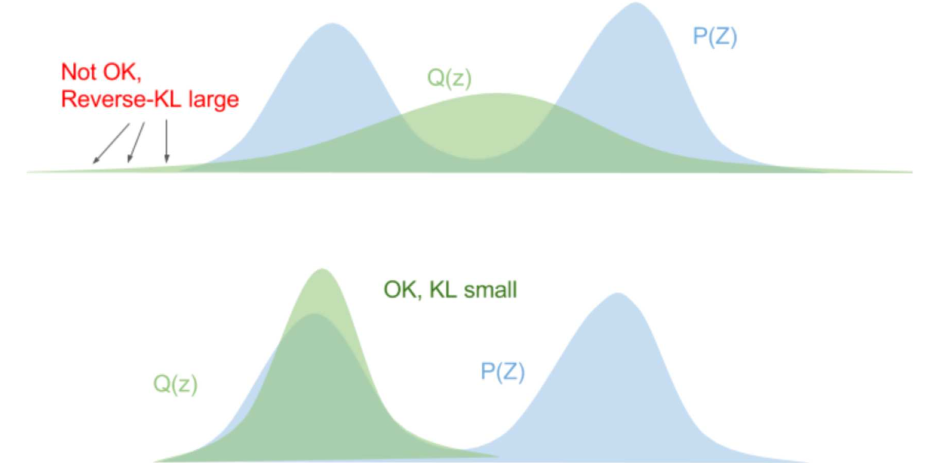
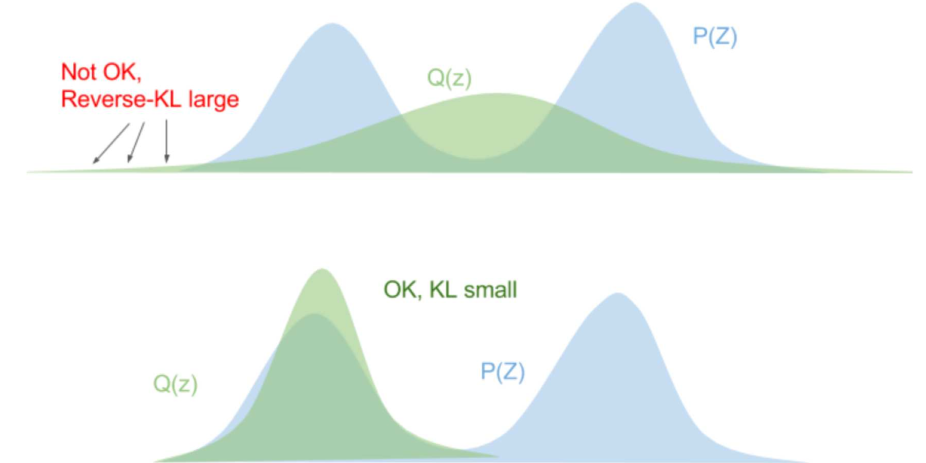
Forward KL-Divergence — when we have a distribution $P$ and we want to choose a Normal distribution $Q$ which is 'close' to $P$, or 'approximately' $P$. In this case, we can use the KL-divergence, $D_{KL}(P \parallel Q)$, as a loss function to minimise.
Reverse KL-Divergence — when we have a distribution $P$ and we want to choose a Normal distribution $Q$ that minimises $D_{KL}(Q \parallel P)$ rather than $D_{KL}(P \parallel Q)$.
| Forward | Reverse |
|---|---|
 |
 |
Cross Entropy in Deep Learning:¶
Cross-entropy is a measure of the relative entropy between two probability distributions over the same set of events.
For classification tasks where the output should be either 0 or 1, the mean squared error loss function works poorly.
Instead, we can use the cross-entropy error function $E=-(t\log (z) + (1-t)\log(1-z))$, where $z$ is the network's probability prediction and $t$ is the target value.
- If $t=1$, $E=-\log (z)$
- If $t=0$, $E=-\log(1-z)$, so if $z\approx 1$, then the loss value is very large
This forces the network to put higher emphasis on misclassifications
- Eg. In the case of detecting credit card fraud, there would be a significantly larger proportion of negative instances than positive instances. Cross-entropy would place greater emphasis on the positive instances it misclassifies, which in this application, is extremely important.
Choosing the cross-entropy error function makes backpropagation computations simpler. Suppose we have the logistic sigmoid activation function: $a=\frac{1}{1+e^{-z}}$. Note how
$$\frac{\partial E}{\partial a}=\frac{a-t}{a(1-a)},$$and applying the chain rule, we have $$\frac{\partial E}{\partial z}=\frac{\partial E}{\partial a}\cdot \frac{\partial a}{\partial z}=a-t,$$
a very simple result.
Note: we use $\log_e$ in the cross-entropy code implementation rather than $\log_2$ since the derivative of $\ln$ is simpler than $\log_2$.